symbol table

主要功能：

插入一个 value-key
给一个 key，查找对应的 value

实现方法：

unordered list
order array with binary search
binary search tree
2-3 tree (通过 red-black bst 实现)

binary search tree

Each node has a key, and every node’s key is:

Larger than all keys in its left subtree.
Smaller than all keys in its right subtree.

插入操作实现，运用递归：

public void put(Key key, Value val) {
    if (val == null) {
        delete(key);
        return;
    }
    root = put(root, key, val);
    assert check();
}

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val, 1);
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = put(x.left,  key, val);
    else if (cmp > 0) x.right = put(x.right, key, val);
    else              x.val   = val;
    x.N = 1 + size(x.left) + size(x.right);
    return x;
}

delete 操作可使用 hibbard deletion 算法（不对称）

red black binary search tree

2-3树：

2-node: one key, two childern.
3-node: two key, three childern.

特点：

symmetric order
perfect balance （解决普通bst最坏的情况）

但是实现复杂，引入红黑树实现。
红黑树 search 操作与 bst 一样;
插入操作：

public void put(Key key, Value val) {
    root = put(root, key, val);
    root.color = BLACK;
    // assert check();
}

// insert the key-value pair in the subtree rooted at h
private Node put(Node h, Key key, Value val) {
    if (h == null) return new Node(key, val, RED, 1);

    int cmp = key.compareTo(h.key);
    if      (cmp < 0) h.left  = put(h.left,  key, val);
    else if (cmp > 0) h.right = put(h.right, key, val);
    else              h.val   = val;

    // fix-up any right-leaning links
    if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
    if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
    if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);
    h.N = size(h.left) + size(h.right) + 1;

    return h;
}

Symbol Table

symbol table

binary search tree

red black binary search tree

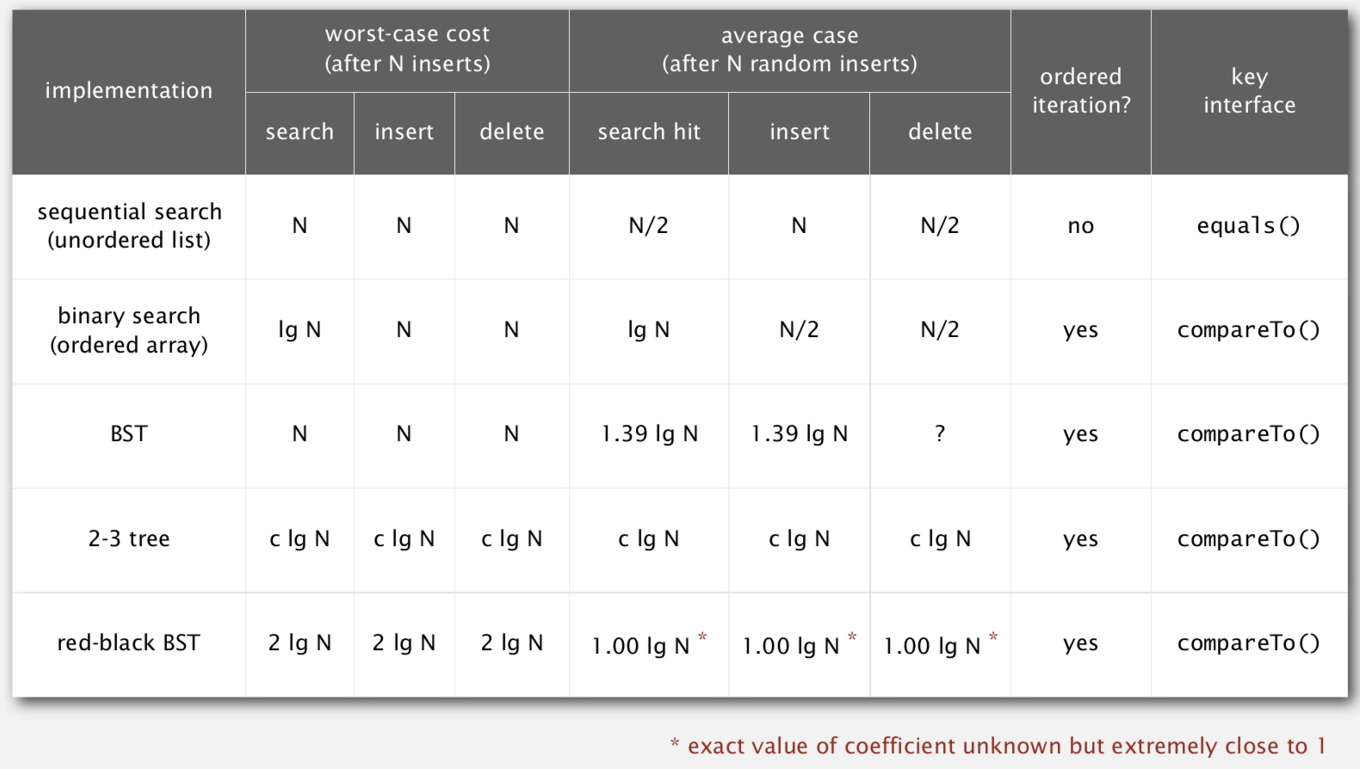
总结