Sort

发表于   |   分类于 ，   |  

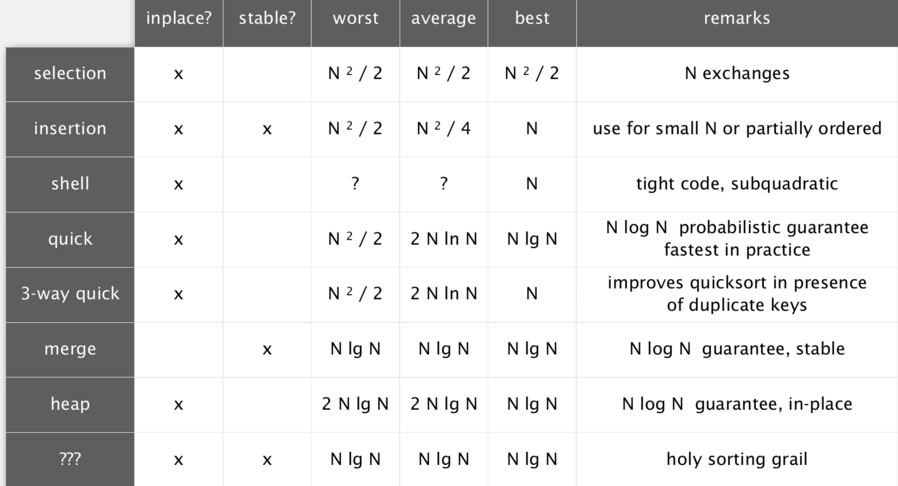
selection sort

insertion sort

merge sort

  1. 基本思想
  • 将数组分成两半
  • 递归排序每一半
  • 合并两半

  1. 具体实现
    见附件 Merge.java

  2. 算法复杂度

  • 时间复杂度：Θ(nlogn)
  • 空间复杂度：需要额外的空间，等价于数组长度
  • 稳定排序
  1. 改进方法
  • 对小数组直接使用插入排序
  • 左半边最大值小于右半边最小值，直接结束排序
  • 消除复制辅助数组（save time not space）

quick sort

  1. 基本思想
  • 打乱数组 (避免快排出现最坏情况)
  • 分块，对于某个元素，元素左边分快中的元素都小于该元素，元素右边分块中的元素都大于该元素
  • 递归排序两个分块
  1. 具体实现
    见附件 Quick.java
  • Partitioning in-place. Using an extra array makes partitioning easier
    (and stable), but is not worth the cost.
  • Terminating the loop. Testing whether the pointers cross is a bit trickier
    than it might seem.
  • Staying in bounds. The (j == lo) test is redundant (why?),
    but the (i == hi) test is not.
  • Preserving randomness. Shuffling is needed for performance guarantee.
  • Equal keys. When duplicates are present, it is (counter-intuitively) better
    to stop on keys equal to the partitioning item’s key.
  1. 特点
  • 时间复杂度：θ(nlogn), best case: nlogn, worst case: $0.5n^2$, average case:1.39nlogn
  • 空间复杂度：并不需要额外的空间
  • 不稳定排序
  1. 改进方法
  • 对小数组直接使用插入排序
  • 选择尽量是中点的分割点：int m = medianOf3(a, lo, lo + (hi - lo)/2, hi);
  1. quick selection
    问题描述: 找到一组数据中第k大的数
1
2
3
4
5
6
7
8
9
StdRandom.shuffle(a);
int lo = 0, hi = a.length - 1;
while (hi > lo) {
    int i = partition(a, lo, hi);
    if (i > k) hi = i - 1;
    else if (i < k) lo = i + 1;
    else  a[i];
}
return a[lo];

平均时间复杂度：θ(n)

heap sort

  1. 基本思想
  • 对排序元素构造最大堆积树
  • 不断移除最大值
  1. 具体实现
    见附件 heap.java
  • build heap using bottum-up method
1
2
for (int k = N/2; k>=1; k--)
    sink(a, k, N);
  • remove the maximum, one at time. leave in array, instead of nulling out.
1
2
3
4
5
while (N>1)
{
    exch(a, 1, N--);
    sink(a, 1, N);
}
  1. 特点
  • in-palce
  • 时间复杂度：θ(NlogN)
  • unstable
  • make poor use of cache memory
    img1